2009-07-04

知識

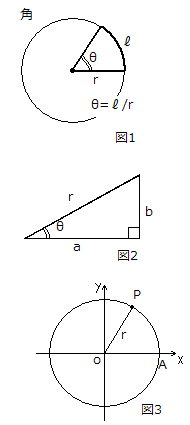
角の定義
[図1]の半径rの円における扇形(太線)において、
弧の長さがlとなるような扇の中心角を
θ=l/rと定義する。
θは長さを長さで割ったものなので無次元であるが、
角度であることを言う為に[rad](ラジアン)という単位をつけることがある。

三角関数
[図2]の直角三角形のように、長さをa,b,r、角度θを設定した時(0<θ<π/2)、
三角比cosθ=a/r
sinθ=b/rを定義する。

今、θは有限の範囲を取る実数であるが、実数全域をとるように
拡大する三角関数を次のように定義する。

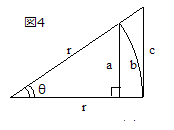
[図3]のxy座標で、原点を中心として半径rの円周上を自由に動く点Pについて
θ=∠POAとすると
点Pの座標は(r･cosθ, r･sinθ)通常は半径r=1の単位円で考える。

基本的性質
sinθ+cosθ=1　---(1)
tanθ=sinθ/cosθ　---(2)
(1)の両辺をcos2θで割れば、
tanθ+1=1/cosθ　---(3)
従って、sinθ,cosθは[-1,1]内の実数、tanθは実数全域を取る。

sinθ、cosθは周期2πの周期関数。
sin(θ+2π)=sinθ　---(4)
cos(θ+2π)=cosθ　---(5)

sin(x)とcos(x)は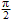ずれており
sin(x+π/2) = cos(x)　---(6)

cos(x)は偶関数
cos(x) = cos(-x)　---(7)
sin(x)は奇関数
sin(-x) = -sin(x)　---(8)

加法定理
幾何学的関係から
sin(α+β) = sinα･cosβ+sinβ･cosα
βの代わりに-βを入れ、(7)と(8)から
sin(α-β) = sinα･cosβ-sinβ･cosα
この二式を纏めると
sin(α士β) = sinα･cosβ士sinβ･cosα　---(9)
また、
cos(α+β) = cosα･cosβ-sinα･cosβ
βの代わりに-βを入れ、(7)と(8)から
cos(α-β) = cosα･cosβ+sinα･cosβ
この二式を纏めると
cos(α士β) = cosα･cosβ干sinα･sinβ　---(10)
また、
tan(α士β) = {tanα士tanβ}/{1干tanα･tanβ}　---(11)

加法定理は基本事項の中の最も重要な事項である。以下では、断り無く用いる。

二倍角の公式
(9)の複号の上の式でα=βを用いれば
sin2α = 2sinα･cosα　---(12)
(10)の複号の上の式でα=βを用いれば
cos2α = cosα-sinα　---(13)
これに(1)を用いると
cos2α = 2cosα-1 = 1-2sinα　---(14)

半角の公式
(14)のcos2α = 1-2sin2α にA=2αを代入すると
cosA = 1-2sin(A/2) ⇔ sin(A/2) = (1-cosA)/2　---(15)

(14)のcos2α = 2cos2α-1 にA=2αを代入すると
cosA = 2cos(A/2)-1 ⇔ cos(A/2) = (1+cosA)/2　---(16)

三倍角の公式
sin3α = sin(2α+α)
　　　 = sin2α･cosα+cos2α･sinα
　　　 = 2sinα･cosα･cosα+(1-2sinα)･sinα
　　　 = 2sinα(1-sinα+1-2sinα)
　　　 = 3sinα-4sin3α　---(17)

cos3α = cos(2α+α)
　　　 = cos2α･cosα-sin2α･sinα
　　　 = (2cosα-1)cosα-2sinαcosα
　　　 = (2cosα-1-2(1-cosα))cosα
　　　 = 4cos3α-3cosα　---(18)

和積の交換
この小章では
　A=α+β, B=α-β
とする。

(9)の複号の上の式と下の式を足せば
sin(α+β)+sin(α-β) = 2sinα･cosβ　---(19)
⇔ sinA+sinB = 2sin{(A+B)/2}･cos{(A-B)/2}　---(20)

(10)の複号の上の式と下の式を足して
cos(α+β)+cos(α-β) = 2cosα･cosβ　---(21)
⇔ cosA+cosB = 2cos{(A+B)/2}･cos{(A-B)/2}　---(22)

(10)の複号の下の式から上の式を引いて
cos(α-β)-cos(α+β) = 2cosα･sinβ　---(23)
⇔ cosB-cosA = 2sin{(A+B)/2}･sin{(A-B)/2}　---(24)

sinとcosの交換
(6)よりsin(x+π/2) = cos(x)であるが、x→x-π/2の変数変換を施すと
sin(x) = cos(x-π/2)
cos(x)は偶関数であり、cosθ=cos(-θ)であることから
sin(x) = cos(π/2-x)　---(25)
また、x→π/2-xの変数変換をすると
sin(π/2-x) = cos(x)　---(16)

このように、sin,cosをcos,sinに単純に変換することができる。

三角関数の合成
直角の挟辺がa,bとなるような直角三角形を考える。
辺aの2隣角の直角でない方をαとする。(α<π/2)
この時
cosα = a/√(a+b), sinα = b/√(a+b)
となるから、
a･sin(x)+b･cos(x) = √(a+b) cosα･sin(x)+√(a+b) sinα･cos(x)
　　　　　　　　　= √(a+b)･sin(x+α)　---(27)

三角数を含む方程式
#sin(x)=0 ⇔ x=nπ(nは整数)

#cos(x)=0 ⇔ x=π/2+nπ(nは整数)

#sin(x)=1 ⇔ x=π/2+2nπ(nは整数)

#cos(x)=1 ⇔ x=2nπ(nは整数)

#sin(x)+sin(y)=0
⇔ 2sin{(x+y)/2}･cos{(x-y)/2}=0
∴sin{(x+y)/2}=0またはcos{(x-y)/2}=0
⇔ (x+y)=2nπまたは(x-y)=(2n+1)π
⇔ y = -x+2nπ
または
　 y = x-(2n+1)π　　　(但しnは整数)

#a･sin(x)+b･cos(x)=0
⇔√(a+b)･sin(x+α)=0 (ただし、αはtanα=b/aを満たす)
∴sin(x+α)=0
⇔x=nπ-α
　　=nπ-tan-1(b/a)

極限
右図4のような扇とそれに内接、外接する直角三角形を考える。

内接する直角三角形の面積 S1
扇の面積 S2
外接する直角三角形の面積 S3　は
S1<S2<S3
を満たすのは図より明らか。
S1 = 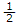r･a
S2 = 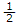r･b
S3 = 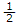r･c

a = r･sinθ
b = rθ
c = r･tanθ

∴ sinθ<θ<tanθ (0<θ<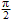)　---(28)
(28)より 0<θ<について
sinθ<θ⇔sinθ/θ<1
θ<tanθ⇔cosθ<sinθ/θ
∴cosθ<sinθ/θ<1
θ→0に飛ばす時、cosθ→1なので挟み撃ちによって
sinθ/θ→1 (θ→0)　---(29)

また(28)より 0<θ<について
θ<tanθ⇔1<tanθ/θ
sinθ<θ⇔tanθ/θ<1/cosθ
∴1<tanθ/θ<1/cosθ
θ→0に飛ばす時、1/cosθ→1なので挟み撃ちによって
tanθ/θ→1 (θ→0)　---(30)

微分
{sin(x+h)-sin(x)}/h = {sin(x)･cos(h)+sin(h)･cos(x)-sin(x)}/h
　　　　　　　　　　= {sin(x)･(cos(h)-1)+cos(x)･sin(h)}/h
　　　　　　　　　　= sin(x)･(cos(h)-1)/h + cos(x)･sin(h)/h
　　　　　　　　　　→ 0+cos(x)･1 = cos(x) (h→0)
微分の定義から
{sin(x)}' = cos(x)　---(31)
更に、(26)を用いれば
{cos(x)}' = {sin(π/2-x)}'
　　　　　= -cos(π/2-x)
　　　　　= -sin(x)
{cos(x)}' = -sin(x)　---(32)

(31)と(32)を使えば
{tan(x)}' = 1/cos2(x)

テイラー展開
x〜0の周りでのテイラー展開
f(x)〜f(0)+f'(0)･x+f"(0)･x2/2!+ … +f(n)(0)･xn/n!+ …
を用いれば
sin(x)〜x-x3/3!+x5/5!-x7/7!+ …　---(33)
cos(x)〜1-x2/2!+x4/4!-x6/6!+ …　---(34)
|x|が十分小さければxの二次以上を無視して
sin(x)≒x　---(35)
cos(x)≒1　---(36)

積分



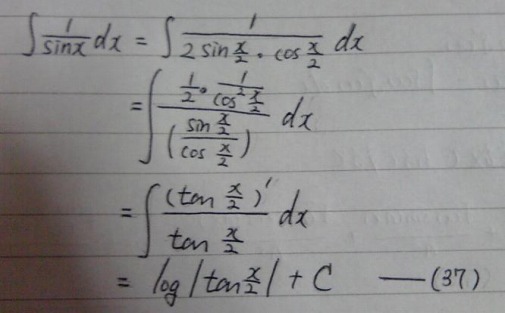
○例題


部分積分
{f(x)g(x)}'=f'(x)g(x)+f(x)g'(x)
　⇔　∫f'(x)g(x) = f(x)g(x)-∫f(x)g'(x)dx
を繰り返し用いれば

f(x)がn次以下の整式の時、


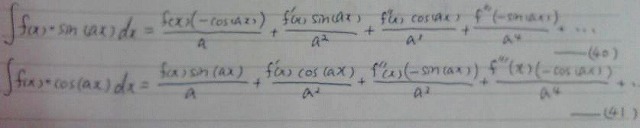sinθ1やcosθ2が混在する式は
和積変換の公式により和に直せば積分計算が楽になる。

更に積分結果がA･sinθ1+B･cosθ1+C･sinθ2+D･cosθ2 になることを期待して、
コレを微分してABCDを求めてもよい。
(c)Kero's World