���l�����Ɛ��l�ϕ�
��f(x)�̂���x=a�ł�f'(a),f"(a)�𐔒l�I�ɋߎ��v�Z������B
�����̒�`��
�@f'(a) = lim[h��0] (f(a+h) - f(a))/h
������ߎ�����̂�
�@lim[h��0] h = ��x
���p����悢�A�ƍl����̂����l�����̊�{�I�Ȕ��z�ł���B
���̂悤�ɑO�������A��������A���S�������`����B
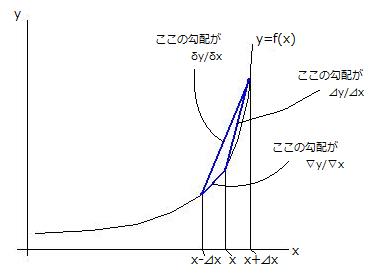 �O������(forward difference)
�@��y/��x = (f(x+��x) - f(x))/��x
��������܂��͌�ލ���(backward difference)
�@��y/��x = (f(x) - f(x-��x))/��x
���S����(central difference)
�@��y/��x = (f(x+��x) - f(x-��x))/2��x
����́A��y/��x�Ɓ�y/��x�̕��ςƂȂ�B
�e�C���[�W�J�����Ă݂�
�@f(x+��x) = f(x)+f'(x)��x/1!+f"(x)(��x)2/2!+ �c +f(n)(��x)n/n!+ �c
���ꂩ��
�@{f(x+��x)-f(x)}/��x = f'(x)/1!+f"(x)(��x)1/2!+ �c +f(n)(��x)n-1/n!+ �c
�@����x/��y = f'(x)+f"(x)(��x)1/2!+ �c +f(n)(��x)n-1/n!+ �c
���l��
�@f(x-��x) = f(x)-f'(x)��x/1!+f"(x)(��x)2/2!+ �c -f(n)(��x)n/n!+ �c
���ꂩ��
�@{f(x)-f(x-��x)}/��x = f'(x)/1!-f"(x)(��x)1/2!+ �c +f(n)(��x)n-1/n!+ �c
�@����x/��y = f'(x)-f"(x)(��x)1/2!+ �c +f(n)(��x)n-1/n!+ �c
n�K���W���̋ߎ�
��̃e�C���[�W�J��������p����B
�ǂݔ�����҂͌���(������)�����ł�����悤�ɁB
�@��y/��x-��y/��x = f"(x)��x+f""(x)(��x)2/2�4!+ �c
�������x�Ŋ����
�@(��y/��x-��y/��x)/��x = f"(x)+f""(x)��x+ �c
f""(x)��x�ȏ�̍��͏������̂Ŗ��������
(��y/��x-��y/��x)/��x��f"(x)�̋ߎ��Ƃł���B
�܂��A�����
�@��2y/��x2�ƕ\���A2�K�̒��S�����Ƃ����B
�O������(forward difference)
�@��y/��x = (f(x+��x) - f(x))/��x
��������܂��͌�ލ���(backward difference)
�@��y/��x = (f(x) - f(x-��x))/��x
���S����(central difference)
�@��y/��x = (f(x+��x) - f(x-��x))/2��x
����́A��y/��x�Ɓ�y/��x�̕��ςƂȂ�B
�e�C���[�W�J�����Ă݂�
�@f(x+��x) = f(x)+f'(x)��x/1!+f"(x)(��x)2/2!+ �c +f(n)(��x)n/n!+ �c
���ꂩ��
�@{f(x+��x)-f(x)}/��x = f'(x)/1!+f"(x)(��x)1/2!+ �c +f(n)(��x)n-1/n!+ �c
�@����x/��y = f'(x)+f"(x)(��x)1/2!+ �c +f(n)(��x)n-1/n!+ �c
���l��
�@f(x-��x) = f(x)-f'(x)��x/1!+f"(x)(��x)2/2!+ �c -f(n)(��x)n/n!+ �c
���ꂩ��
�@{f(x)-f(x-��x)}/��x = f'(x)/1!-f"(x)(��x)1/2!+ �c +f(n)(��x)n-1/n!+ �c
�@����x/��y = f'(x)-f"(x)(��x)1/2!+ �c +f(n)(��x)n-1/n!+ �c
n�K���W���̋ߎ�
��̃e�C���[�W�J��������p����B
�ǂݔ�����҂͌���(������)�����ł�����悤�ɁB
�@��y/��x-��y/��x = f"(x)��x+f""(x)(��x)2/2�4!+ �c
�������x�Ŋ����
�@(��y/��x-��y/��x)/��x = f"(x)+f""(x)��x+ �c
f""(x)��x�ȏ�̍��͏������̂Ŗ��������
(��y/��x-��y/��x)/��x��f"(x)�̋ߎ��Ƃł���B
�܂��A�����
�@��2y/��x2�ƕ\���A2�K�̒��S�����Ƃ����B
#include <stdio.h>
#include <math.h>
#define dx (0.1) //��x
/**
* x�̊�f(x)�ɂ���
* f"(a)�̋ߎ��l�����߂�B
* ----
* �����ł�
* f(x)=x^3
* f"(x)=6x�̃n�Y�����c
*/
float f(float x){
return pow(x,3); //f(x)=x^3
}
main(){
float x,fpp;
for(x=0;x<10;x++){
fpp=(f(x+dx)-2*f(x)+f(x-dx))/dx/dx;
printf("f\"(%1.0f) = %f\n",x,fpp);
}
}
f(x)=x3�Ƃ������ɂ���
f"(x)�����߂Ă���B
���͒P���Ȃ̂Ńv���O�����ɔC����܂ł��Ȃ��A
f"(x)=6x�Ƃ킩��B
���ۂɃv���O�����ŁA
f"(0)�Af"(1)�Af"(2) �c f"(9)
�̌v�Z���ʂ�\�����Ă���B
0,6,12,18,,,54
�ƁA�o�͂����Ί��S�����c
�덷�͇�x(�v���O�����ł�dx)�̓��ɔ�Ⴗ��B
�����A��������Ώ�������(���_��)�����ɂȂ邪�A����͌�����
������ł�����ꍇ�����ŁAf(x+��x)-f(x)�̌��ʂ�0�△�Ӗ���
���l�ɂȂ��Ă��܂��B
��ʂ̏ꍇ
��ny/��xn�ɂ��Ă�(n���m)
n�������̎�
�@��ny/��xn = {(��n-2y/��(x+��x)n-2) - 2(��n-2y/��xn-2) + (��n-2y/��(x-��x)n-2)}/��x2
n����̎�
�@��ny/��xn = {(��n-1y/��(x+��x)n-1) - (��n-1y/��(x-��x)n-1)}/2��x
������X�^�[�����O(Stirling)�̕����Ƃ����B
���l�ϕ�
��ϕ��͎��̂悤�ɕ\����
�@��[a�`b] f(x)�dx = lim[n����](b-a)/n��[k=1�`n]f(a+k(b-a)/n)
�Ə�����lim[n����]n�̑���Ɂu�\���傫��n�v���g�����Ƃŋߎ�����B
��ϕ��͉��̐}�̐F�̎ΐ��̖ʐς����߂邱�ƂɂȂ�B
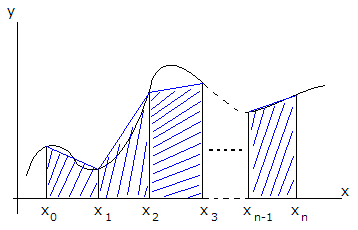 x��a�`b��n�������A�[����x0(=a)�Ax1�Ax2�A�cxn-1�Axn(=b)�Ƃ���B
xk��a+k(b-a)/n�ł���B
�܂��A��������x�̕�����x�Ƃ���B
�@��x = (b-a)/n = xn-xn-1
����āA
�@I = ����x*{f(xn)+f(xn+1)}/2
��f(x)=4/(1+x2)��x�̒�`��[0�`1]��dx�Őϕ�����B
x=tan�ƂƂ���B
�@1/(1+x2)=cos2��
�@dx=1/cos2��
�ł��邩��A
��f(x)�dx = ��1�d��
�@�@�@�@�@= ��
x��a�`b��n�������A�[����x0(=a)�Ax1�Ax2�A�cxn-1�Axn(=b)�Ƃ���B
xk��a+k(b-a)/n�ł���B
�܂��A��������x�̕�����x�Ƃ���B
�@��x = (b-a)/n = xn-xn-1
����āA
�@I = ����x*{f(xn)+f(xn+1)}/2
��f(x)=4/(1+x2)��x�̒�`��[0�`1]��dx�Őϕ�����B
x=tan�ƂƂ���B
�@1/(1+x2)=cos2��
�@dx=1/cos2��
�ł��邩��A
��f(x)�dx = ��1�d��
�@�@�@�@�@= ��
#include <stdio.h>
/**
* f(x) = 4/(1+x^2)�̐ϕ�
*/
float f(float x){
return 4/(1+x*x);
}
main(){
float k,n,a,b;
float sum=0.0,dx;
printf("������ n=");scanf("%f",&n);
a=0;b=1;
dx=(b-a)/n;
for(k=0;k<n;k++){
sum += dx * (f(a+(b-a)*k/n)+f(a+(b-a)*(k+1)/n))/2;
}
printf("��4/(1+x^2)�dx = %f",sum);
}
���߂�n���w�肷��B
256�Ƃ����3.141590�ƕ\������A��̃ƂȂ�B
���Ȃ݂ɁAk,n,a,b��int�^�ł������悤�ȋC�����邪
dx=(b-a)/n
��(a+(b-a)*k/n)
���A�����int�ɔ����A���������ϐ��̑O��(float)������̂�
�ʓ|�Ȃ̂ŁA���߂�float�^�Ő錾�����B
�Q�l�F��g�o�Ł@�u�������R�[�X7�@���l�v�Z�v�ː씹�l��
goto index
 �O������(forward difference)
�@��y/��x = (f(x+��x) - f(x))/��x
��������܂��͌�ލ���(backward difference)
�@��y/��x = (f(x) - f(x-��x))/��x
���S����(central difference)
�@��y/��x = (f(x+��x) - f(x-��x))/2��x
����́A��y/��x�Ɓ�y/��x�̕��ςƂȂ�B
�e�C���[�W�J�����Ă݂�
�@f(x+��x) = f(x)+f'(x)��x/1!+f"(x)(��x)2/2!+ �c +f(n)(��x)n/n!+ �c
���ꂩ��
�@{f(x+��x)-f(x)}/��x = f'(x)/1!+f"(x)(��x)1/2!+ �c +f(n)(��x)n-1/n!+ �c
�@����x/��y = f'(x)+f"(x)(��x)1/2!+ �c +f(n)(��x)n-1/n!+ �c
���l��
�@f(x-��x) = f(x)-f'(x)��x/1!+f"(x)(��x)2/2!+ �c -f(n)(��x)n/n!+ �c
���ꂩ��
�@{f(x)-f(x-��x)}/��x = f'(x)/1!-f"(x)(��x)1/2!+ �c +f(n)(��x)n-1/n!+ �c
�@����x/��y = f'(x)-f"(x)(��x)1/2!+ �c +f(n)(��x)n-1/n!+ �c
n�K���W���̋ߎ�
��̃e�C���[�W�J��������p����B
�ǂݔ�����҂͌���(������)�����ł�����悤�ɁB
�@��y/��x-��y/��x = f"(x)��x+f""(x)(��x)2/2�4!+ �c
�������x�Ŋ����
�@(��y/��x-��y/��x)/��x = f"(x)+f""(x)��x+ �c
f""(x)��x�ȏ�̍��͏������̂Ŗ��������
(��y/��x-��y/��x)/��x��f"(x)�̋ߎ��Ƃł���B
�܂��A�����
�@��2y/��x2�ƕ\���A2�K�̒��S�����Ƃ����B
�O������(forward difference)
�@��y/��x = (f(x+��x) - f(x))/��x
��������܂��͌�ލ���(backward difference)
�@��y/��x = (f(x) - f(x-��x))/��x
���S����(central difference)
�@��y/��x = (f(x+��x) - f(x-��x))/2��x
����́A��y/��x�Ɓ�y/��x�̕��ςƂȂ�B
�e�C���[�W�J�����Ă݂�
�@f(x+��x) = f(x)+f'(x)��x/1!+f"(x)(��x)2/2!+ �c +f(n)(��x)n/n!+ �c
���ꂩ��
�@{f(x+��x)-f(x)}/��x = f'(x)/1!+f"(x)(��x)1/2!+ �c +f(n)(��x)n-1/n!+ �c
�@����x/��y = f'(x)+f"(x)(��x)1/2!+ �c +f(n)(��x)n-1/n!+ �c
���l��
�@f(x-��x) = f(x)-f'(x)��x/1!+f"(x)(��x)2/2!+ �c -f(n)(��x)n/n!+ �c
���ꂩ��
�@{f(x)-f(x-��x)}/��x = f'(x)/1!-f"(x)(��x)1/2!+ �c +f(n)(��x)n-1/n!+ �c
�@����x/��y = f'(x)-f"(x)(��x)1/2!+ �c +f(n)(��x)n-1/n!+ �c
n�K���W���̋ߎ�
��̃e�C���[�W�J��������p����B
�ǂݔ�����҂͌���(������)�����ł�����悤�ɁB
�@��y/��x-��y/��x = f"(x)��x+f""(x)(��x)2/2�4!+ �c
�������x�Ŋ����
�@(��y/��x-��y/��x)/��x = f"(x)+f""(x)��x+ �c
f""(x)��x�ȏ�̍��͏������̂Ŗ��������
(��y/��x-��y/��x)/��x��f"(x)�̋ߎ��Ƃł���B
�܂��A�����
�@��2y/��x2�ƕ\���A2�K�̒��S�����Ƃ����B
 x��a�`b��n�������A�[����x0(=a)�Ax1�Ax2�A�cxn-1�Axn(=b)�Ƃ���B
xk��a+k(b-a)/n�ł���B
�܂��A��������x�̕�����x�Ƃ���B
�@��x = (b-a)/n = xn-xn-1
����āA
�@I = ����x*{f(xn)+f(xn+1)}/2
��f(x)=4/(1+x2)��x�̒�`��[0�`1]��dx�Őϕ�����B
x=tan�ƂƂ���B
�@1/(1+x2)=cos2��
�@dx=1/cos2��
�ł��邩��A
��f(x)�dx = ��1�d��
�@�@�@�@�@= ��
x��a�`b��n�������A�[����x0(=a)�Ax1�Ax2�A�cxn-1�Axn(=b)�Ƃ���B
xk��a+k(b-a)/n�ł���B
�܂��A��������x�̕�����x�Ƃ���B
�@��x = (b-a)/n = xn-xn-1
����āA
�@I = ����x*{f(xn)+f(xn+1)}/2
��f(x)=4/(1+x2)��x�̒�`��[0�`1]��dx�Őϕ�����B
x=tan�ƂƂ���B
�@1/(1+x2)=cos2��
�@dx=1/cos2��
�ł��邩��A
��f(x)�dx = ��1�d��
�@�@�@�@�@= ��