f(x) = 0 を解くには x = (xを含まない数式) という形に変形すればよいが実際にはいつもこの形に変形できるとは限らない。 その場合にコンピュータを用いて近似値を求めてみる。 直接探索法 関数f(x)のグラフを描き、x軸と交わる点を探す。 例としてx-cos(x)=0を解いてみる。 f(x) = x-cos(x) とおけば、 求めるxはf(x)がx軸と交わる点のx座標となる。 グラフを書いてみると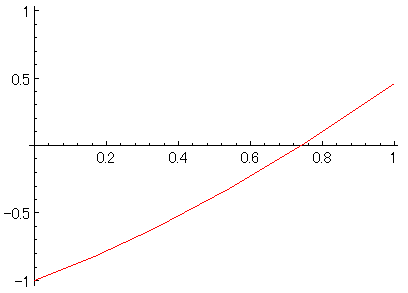だいたい0.75くらい、と分かる。 これをコンピュータが見つけるには、「符号が変わる区間」を探させばよい。 この場合、求めるxより左側ではマイナスで右側ではプラスとなっている。 ズーミング 符号が変わる区間を見つけたらその区間を幾つかの区間に分割して 更にその区間のどこで符号が変わっているかを調べる。 いきなり細かく(例えば1000個に)分割するのは賢明ではなく、まず粗く分割して該当した区間を繰り返し粗く分割する。 例えば、今n等分する時、初めの分割した区間の幅をh[1]とする。 その中の該当する区間をもう一度n等分した区間の幅をh[1]とすれば m回分割した時、区間の幅はh[m]=(1/n)mh[0]となる。 最終的なh[m]がh[0]の100万分の１になる場合を考えると (1/n)m = 10-6 ⇔ m = 6/log(n) （底は10） 分割するのに作る点の数は N=(n-1)m+2 となる。n=2,3,4...についてNを計算してみると
| n | 2 | 3 | 4 | 5 | 10 |
|---|---|---|---|---|---|
| N | 22 | 28 | 32 | 37 | 56 |
#include <stdio.h> #include <math.h> float f(float x){ return x-cos(x); //実際に解く式 } int nibun(float,float); //二分した区間のどちらが適切か判断する main(){ int i; float xr,xl, xm; printf("初めの区間の左端xlと右端xrを入力\n"); printf("xr = "); scanf("%f",&xr); printf("xl = "); scanf("%f",&xl); for(i=0;i<100;i++){ xm=(xl+xr)/2; if(nibun(xl,xr)){ //もし1が戻ってきたら xl=xm; }else{ //0が戻ってきたら xr=xm; } printf("%3d: %f\n",i,xm); } } int nibun(float xl, float xr){ float xm=(xl+xr)/2;//中間点 if(f(xr)*f(xm)<0)return 1;//中間点より右側に求める点がある else return 0; //左側 }
nibun()を100回呼び出してその度にxmを出力しています。 初めにxl=-1, xr=1と入力したところ、 20回目から0.739085に収束した。 今回は二分する点としてxm=(xl+xr)/2、即ち中点を用いたがxm = (xr･f(xl) - xl･f(xr))/(f(xl) - f(xr))
を用いるregula falsi法がある。が、実はこれは効率がよくない。 逐次近似法 解xを求める場合 粗い近似値x[1]から出発し、これを基に、少し精度を高くしたx[2]を 作ることを考える。 即ち、 x[k+1] = φ(x[k]) という関数φ（というかアルゴリズム）を考える。 [例1] 初めの式が x-f(x)=0 という形のとき、 x[k+1]=f(x[k]) を繰り返してけば、大抵解ける(ものに拠る)。 このやり方を逐次代入法と呼ぶ。 [例2] 初めの式が ax+b+f(x)=0 の時、 x=-(b+f(x))/a と、移項して x[k+1]=-(b+f(x[k]))/a を反復すればよい。[例1]と似てるね。 [例3] 高次の整式 f(x)=Σanxn = 0 f(x)はm次式とする。 amxm = g(x) amで割り、両辺をm乗根を取って x=h(x) これを x[k+1] = h(x[k]) という逐次近似式として反復する。 [例1]を用いてx-cos(x)=0を解いてみる。#include <stdio.h> #include <math.h> main(){ int i; float x; printf("初期近似値を入力\nx[0] = "); scanf("%f",&x); for(i=0;i<100;i++){ x=cos(x); //x[k+1]=f(x[k])に当たる。 printf("%3d: %f\n",i,x); } }
x[0]に1を代入してみると、32回目で0.739085に収束した。 試しに100回やってみたが、一般には収束が遅いので、 ・ |x[k+1]-x[k]| がε(適当な小さい定数)未満になったら、収束とみなして終了する ・ 最大反復回数を設定し、それを超えたら収束セズとして終了する これを考慮したのが次のコード#include <stdio.h> #include <math.h> #define ep 0.000001 //ε #define KMAX 2000 //最大反復回数 int main(){ int i; float x,old_x; printf("初期近似値を入力\nx[0] = "); scanf("%f",&x); for(i=0;i<KMAX;i++){ old_x=x; //1つ前のxはold_xに入れる x=cos(x); //x[k+1]=f(x[k])に当たる。 printf("%3d: %f\n",i,x); if(x-old_x<ep&x-old_x>-ep)return 1;//収束 } return 0;//収束セズ } //（やっぱりコード短いなぁ
ニュートン法 皆大好きニュートン法(テイラー展開の1次近似)。 f(x)=0となるxを解く時、 適当な定数aを用いて f(x)〜f(a)+f'(a)(x-a) （※"〜"というのはxがaに極限に近づけば等しくなる、という意味。 ここで、f(x)=0であるから x = a-( f(a)/f'(a) ) この式をx=φ(a)という表せるφがある。 逐次代入を用いれば 適当なx[0]を設定して x[k+1] = x[k] - (f(x[k])/f'(x[k])) x[m→∞]=x 一松法 2次近似を用いると高い精度と早い収束が期待できる。 f(x)〜f(a)+f'(a)(x-a)+f"(a)(x-a)2/2 これを(x-a)について解くと (x-a) = {-f'(a)±sqrt( (f'(a))2 - 2f(a)･f'(a))}/f"(a) さらに x = a+ {-f'(a)±sqrt( (f'(a))2 - 2f(a)･f'(a))}/f"(a) 同様にして x[0]を設定して x[k+1] = x[k]+ {-f'(x[k])±sqrt( (f'(x[k]))2 - 2f(x[k])･f'(x[k]))}/f"(x[k]) x[m→∞]=x ミューラー法 導関数が簡単に計算できない場合は f(x[k-2])、f(x[k-1])からf(x[k])を算出する式を利用する。 その代表的な公式がミューラー法(Muller's method)で、次のように計算する。 上から順に変数を計算していく。 λ=(x[k]-x[k-1])/(x[k-1]-x[k-2]) δ=λ+1 g =f(x[k-2])λ2-f(x[k-1])δ2+(λ+δ)f(x[k]) μ=-2f(x[k])δ/{g±sqrt( g2-4f(x[k])δλ{λf(x[k-2])-δf(x[k-1])+f(x[k])} )} とする。と x[k]=x[k-1]+(f(x[k-1])-f(x[k-2]))μ を逐次代入デ計算する。int main(){char *a="式が複雑なだけなので、コードは略";}
デフレーション 非線形方程式の解は１個とは限らない。 ある一つの解αが求まった後、 f(x)=0 の１解x=α 残りの解を求めるには、 g(x)=f(x)/(x-α) として g(x)=0 を解けばよい。 さらにx=βが求まったら、今度は h(x)=f(x)/(x-α)(x-β) h(x)=0 を解く。このような操作をデフレーション(deflation)という。 精度の保証 近似解^xが求まったら、適当な小さい定数εを決めて f(^x+ε)･f(^x-ε) < 0 (異符号) を確認する。 ただし、この計算自体に誤差がある可能性も考えて f(^x+2ε)･f(^x-2ε) < 0 f(^x+3ε)･f(^x-3ε) < 0 についても確認すべきである